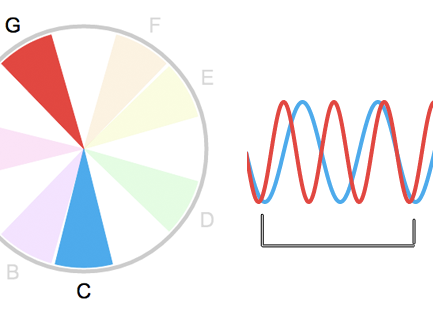
A harmonia é descrita nos livros de música tradicionais como ‘a arte de combinar os sons’, sobretudo quando tocados simultaneamente (ou ‘verticalmente’, já que as notas simultâneas, na pauta, são escritas uma em cima da outra).
Pra entender como as notas se combinam umas com as outras, de modo mais geral, primeiro vamos tentar entender como elas se combinam duas a duas. O quanto duas notas se combinam é uma “grandeza” conhecida como consonância.
Quanto mais consonantes são duas notas, mais elas combinam. E a consonância, assim como tudo na música, é relativa. Quero dizer que a consonância entre o G e o C é a mesma que entre o A e o D, e entre o B e o E. Esses intervalos são igualmente consonantes, já que todos têm o mesmo “tamanho”.
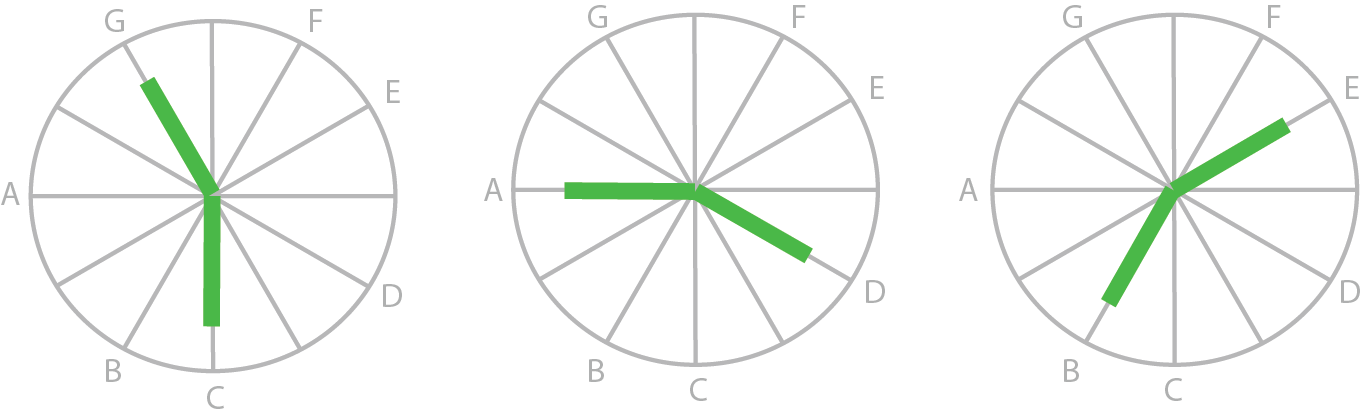
Desse modo, vou limitar os exemplos dados aqui a intervalos entre o Dó e outras notas, mas tenha em mente que basta ‘girar’ o ciclo de notas e tudo se aplica a qualquer outra.
##Combinando Frequências
Então consonância é uma “medida” de quanto duas notas se combinam. Mas o que significa dizer que duas notas “combinam”? Dois sons podem combinar ou descombinar em vários sentidos. No caso específico da harmonia, estamos falando da combinação entre as frequências das notas.
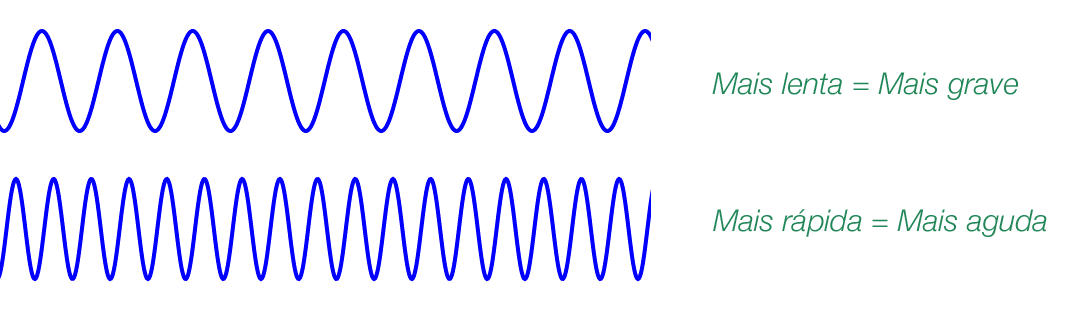
A frequência diz respeito à velocidade de vibração do som. É uma medida normalmente feita em Hertz - vibrações por segundo.
Uma corda de violão mais esticada vibra mais rápido e portanto soa uma nota mais aguda - em uma frequência mais alta.
A consonância entre duas notas significa o quanto as suas frequências ‘combinam’, numericamente falando. Mas mais importante que entender os números é tentar perceber essa relação. Deixe-se tentar expressar essa ‘combinação’ de modo visual.
##Percebendo a Consonância
Dada uma nota, por exemplo um Dó, quais as notas que mais combinam com ela? (Ou a pergunta equivalente: quais os intervalos mais consonantes?)
A nota que mais combina com o Dó é obviamente um outro Dó que vibra exatamente na mesma frequência (imagine dois instrumentos tocando a mesma nota):
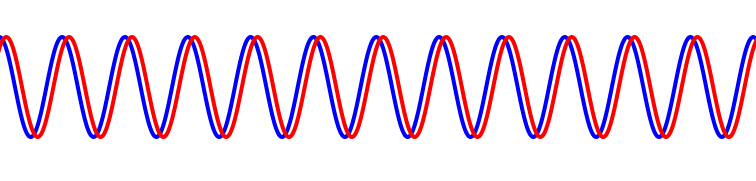
(nessa figura eu desloquei uma das ondas um pouquinho pra vermos melhor as duas linhas…)
Depois dessa, a nota que mais combina com um Dó é o outro Dó uma Oitava acima (ou uma oitava abaixo, dá na mesma!) Essas notas combinam muito porque a frequência do Dó mais agudo é exatamente o dobro da do Dó mais grave:
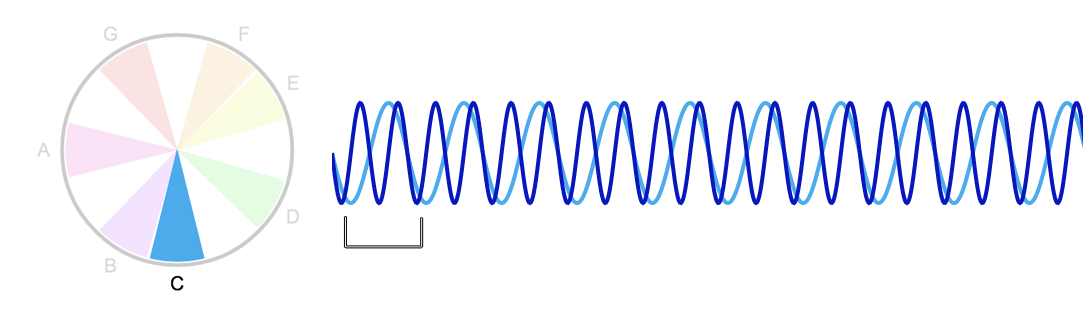
Note que as linhas formam um padrão uniforme, que se repete de modo perfeitamente igual a cada ciclo da nota mais grave, ou a cada dois da nota mais aguda.
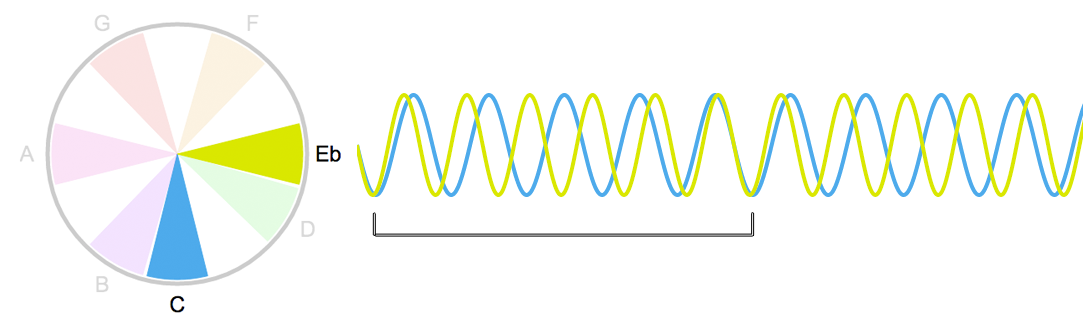
Em seguida, a nota que mais combina com o Dó é o Sol, formando um intervalo de Quinta (Justa).
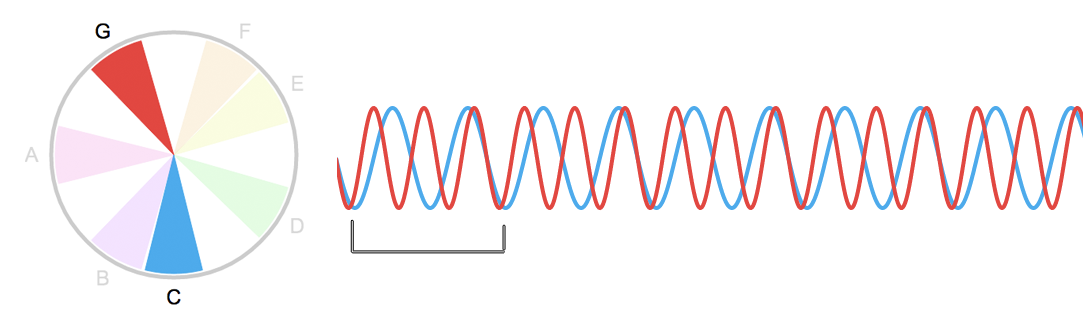
O Sol tem uma frequência 1,5x mais alta que o Dó. Uma vez e meia. O que é o mesmo que dizer que o Sol é 3/2 da frequência do Dó (ou o inverso: que o Dó é 2/3 da frequência do Sol). Dois pra três. Note que as duas linhas se encontram novamente a cada 2 ciclos do Dó (linha azul) ou a cada 3 ciclos do Sol (linha vermelha).
O próximo intervalo mais consonante é o intervalo de Quarta (Justa) que o Dó faz com o Fá:
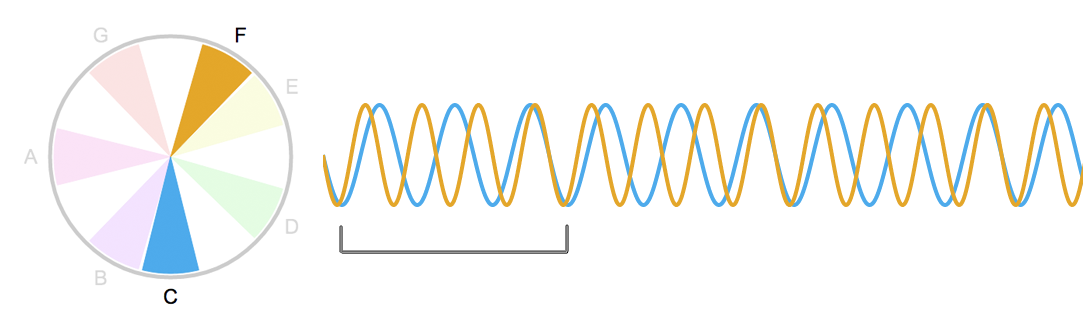
Neste intervalo, as ondas ‘se encontram’ a cada 4 ciclos de uma e a cada 3 ciclos da outra. 4/3.
E assim continua a sequência de intervalos, do mais consonante para o menos consonante: Terça Maior (5/4), depois Terça Menor (6/5) depois Segunda Maior (7/6) e depois Segunda Menor (8/7).
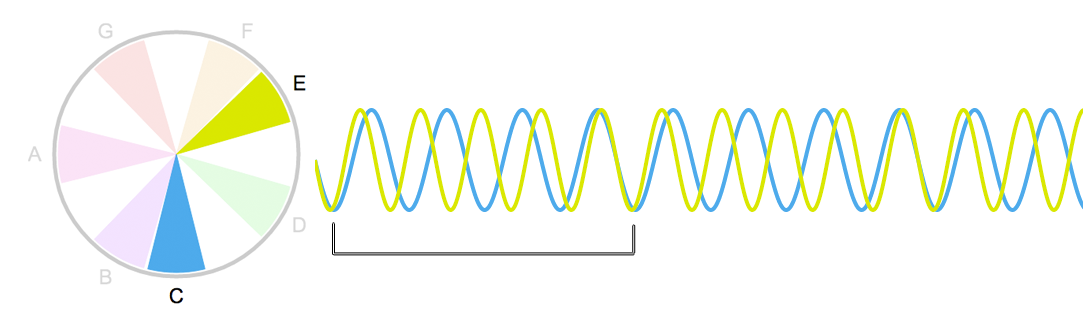
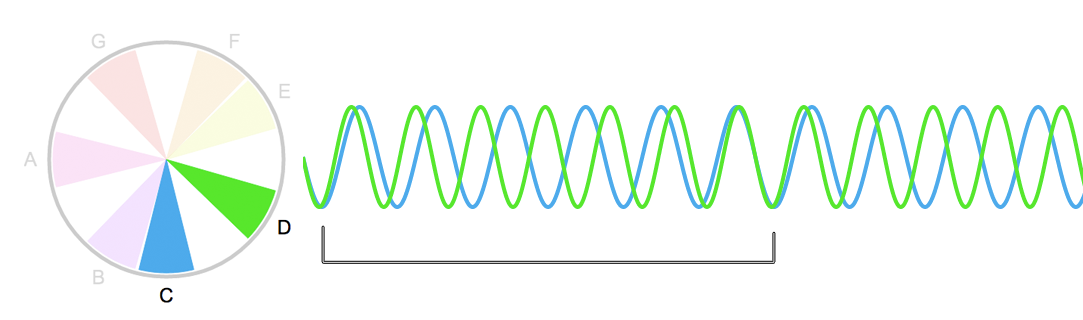
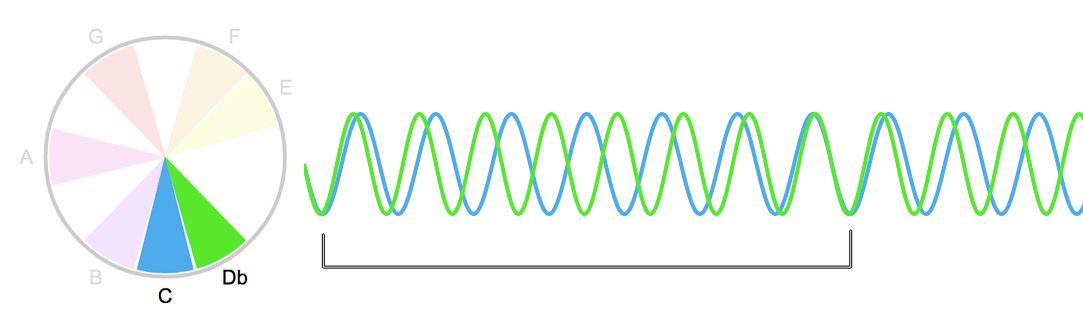
Quanto mais as ondas ‘demoram’ a se encontrar - ou quanto menos elas ‘se encaixam’ - tanto mais desencontradas as notas nos soam. O intervalo de oitava se encaixa tão bem que algumas vezes chegamos a escutar um som só. O de quinta também. O intervalo de segunda menor, no entanto - o equivalente a um semitom - soa destrambelhado! As notas parecem que não encaixam…
Como você deve ter notado, a relação entre as notas dos intervalos, em ordem de consonância, formam um padrão matemático: 1/2, 2/3, 3/4, 4/5, 5/6, 6/7 e 7/8.
Essa sequência é exatamente a sequência de notas que conseguimos extrair de alguns instrumentos, dentro da mesma ‘posição’… O trombone é um exemplo: com a vara na mesma posição, mudando apenas a pressão dos lábio (embocadura), conseguimos emitir exatamente essa sequência de notas. Coincidência?
Essa sequência é o que conhecemos como Série Harmônica.
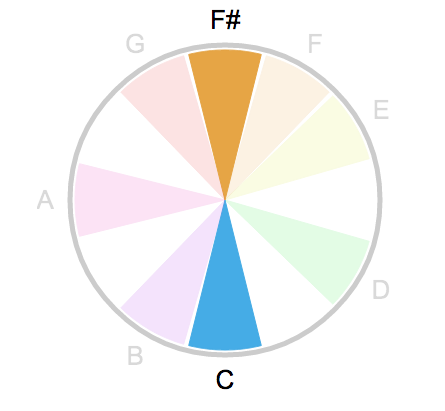
Observe também a sequência de intervalos no ciclo das notas:
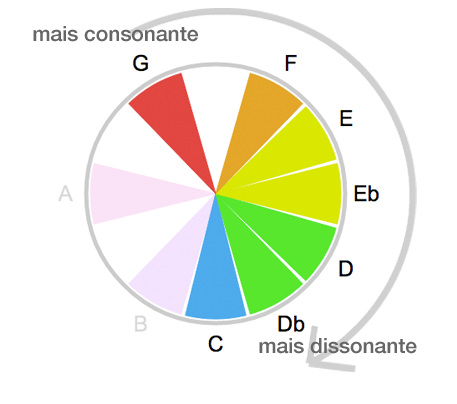
Vamos aos intervalos que ficaram faltando:
O lado esquerdo do ciclo todo cria com a tônica intervalos complementares aos da direita. Então a Sexta Menor, por exemplo, cria com a Tônica um intervalo com exatamente a mesma consonância da Terça Maior (o intervalo complementar). Então eles são tão consonantes quanto seus complementares.
(Sim, a Quinta é o complemento da Quarta - elas são igualmente consonantes!)
O último intervalo que falta é o que corresponde à reta que atravessa o círculo de um lado a outro, num ângulo de 180 graus. Esse intervalo, conhecido como Trítono (por ser formado por 3 tons) é bem importante no estudo da harmonia. Vamos falar mais sobre ele, mas por agora cabe dizer que ele é um dos mais dissonantes de todos
##A arte da dissonância
É bom que se diga: consonância não tem nada a ver com beleza. As dissonâncias bem colocadas ficam lindas! Uma música feita apenas com acordes ‘perfeitos’ fica quadrada, sem graça… A arte é assim: usa combinações (ou descombinações) como temperos para criar um tecido interessante, rico.
Então uma coisa é falar genericamente a respeito de cores. O Amarelo contrapõe o Azul, fazendo com que essas cores conversarem bem. Ponto. Fora de contexto faz todo sentido! Dentro do contexto de uma obra, no entanto, genial é aquele que consegue combinar cores que muitos diriam não combinar… na prática, contexto é tudo e toda regra tem exceção.
É por isso que os acordes ‘complexos’ da bossa nova soam lindos. Sobretudo pelo contexto histórico-social-artístico. Naquele momento histórico, a confusão matemática das dissonâncias fez todo sentido!
Mas nada disso nos faz desconsiderar o papel das consonâncias. A arte quebra as regras - o que reforça o fato de que as regras existem! É justamente por elas existirem que a arte se ocupa em quebrá-las.
Uma coisa é o contexto artístico. Outra é a natureza combinatória, matemática, das ondas sonoras. O Dó se encaixa melhor com o Sol do que com o Ré. Ponto. Se o desencaixe é usado com elegância e torna uma música genial, bem. Mas isso não muda a relação matemática entre as notas.
Matematicamente falando, os intervalos, do mais consonante para o mais dissonante são: Oitava, Quinta Justa, Quarta Justa, Terça maior, Terça menor, Segunda maior e Segunda menor.
##E daí?
O que é que todo esse bla bla bla tem a ver com música? E daí que tal nota combina mais com essa do que com aquela?
A utilidade dessa teoria infelizmente não é tão imediata quanto gostaríamos. Saber quais notas combinam com quais não é o suficiente para que a gente saia compondo belas melodias, criando acordes lindos. Mas é necessário.
A consonância faz parte da base sobre a qual vamos construir a linguagem harmônica. Porque os acordes são formados em tríades de tônica-terça-quinta? Porque o acorde de dominante (5a) contrapõe diretamente o de tônica, criando um padrão de tensão-resolução ao longo da música?
Todas essas coisas constituem uma linguagem que é escrita sobre as letras das notas e seus intervalos, com suas diferentes consonâncias.
Ter familiaridade com intervalos e suas consonâncias vai ser bem útil quando formos falar de acordes e funções harmônicas.